Data Fusion and Reconstruction for Automotive Diagnostics and Control
Instrumented 4-cyclinder, 1.8 litre Nissan petrol engine and transient dynamometer for conducting engine tests
Supervisors: Prof G W Irwin, Dr R Kee and Dr S McLoone
Background
In automotive vehicles, sensors are required to monitor parameters such as temperature, acceleration and pressure. Conventionally, only the measurement of low-frequency temperature variations was required in vehicles. Standard robust sensors such as thermocouples, resistance temperature detectors and thermistors were therefore adequate.
Nowadays, robust temperature sensors with very fast response characteristics are required for control and diagnostics applications including;
- On-board diagnosis (OBD) of catalyst malfunction
- Regeneration of Diesel Particulate Filters (DPF)
- Precision monitoring of exhaust gas temperature in NOx traps
Experimental work at QUB has showed that during transient operation, conventional sensors gave errors of up to 200°C. A reduction in sensor size dramatically improved the accuracy, but in the harsh environment of an exhaust system, a lower limit to the diameter is quickly reached, below which sensor failure occurs.
An alternative approach uses dual sensors with different characteristics, and then mathematically reconstructs the actual gas temperature from the two outputs. We have recently pioneered a novel discrete-time linear identification framework which eliminates the major shortcoming of earlier QUB methods where the dual sensor characteristics must be known a priori. In addition, extensive simulation studies have shown that the new algorithms reduce the sensitivity to noise on the inputs.
The Project
Blind deconvolution, or more correctly blind characterisation in this context, refers to the problem of determining either the input signal or system model or both, given only output measurements. It is already well established for signal processing, telecommunication channel equalisation, image restoration and seismology, but has not previously been applied to sensors.
Our characterisation technique is specifically based on the Cross-Relation method from the field of blind deconvolution. It exploits the commutative relationship between two linear systems to produce a novel two-thermocouple characterisation scheme as illustrated in Fig. 1, where the two measured thermocouple outputs T m1 ( t) and Tm 2 (t) are passed through two synthetic thermocouples represented by first-order filters:
Here is H m1 (s) and Hm2 (s) are the actual thermocouple transfer functions and Tg (t) is the unknown gas temperature. The unknown thermocouple time constants, 
and 
, can then be estimated using the Cross-Relation (CR) method, shown in Figure 1. Here the crossrelation error signal is used to define a mean-square-error (MSE) cost function
Clearly, 
is zero when 
; and 
. In practice, minimising this with respect to
and
yields the required estimates of the true time-constants.
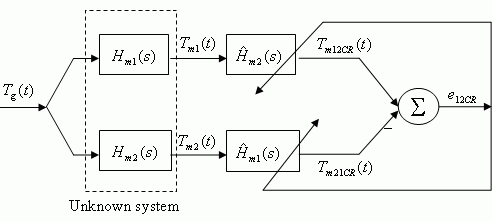
Figure 1. Two-thermocouple Cross-Relation characterisation
The new doctoral project will involve the following:
- Further development of the Cross-Relation method for blind characterisation, including application to experimental data from a test rig and an internal combustion engine, with respect to robustness to noise, speed of convergence, and reconstruction quality.
- Research into alternative Blind Characterisation methods
- Extension of the discrete-time identification frame work to higher-order sensor characterisation
- Generalisation of data fusion to larger numbers of sensors and to other types of engine sensors.
This is an interdisciplinary project in collaboration with the Internal Combustion Engines Research Group, QUB and EE Engineering at Maynooth University. It will require a balanced approach of theoretical development combined with experimental evaluation. A doctoral student in the Internal Combustion Engines Research Group is currently designing sensors and test rigs, as well as investigating the mechanical aspects of the sensors, including the fluid flow and heat transfer around the sensing elements. This will generate the measurement data required to support further algorithmic development, while providing the experimental platform needed for a full experimental evaluation.