Advanced Learning Algorithm for Microarrary Data Analysis
Researchers: Miss Xiao-Lei (Celina) Xia, Prof Xiao-Ou Li, Prof De-Shuang Huang and Dr. Kang Li
Introduction
Computational biology has in recent years emerged as a new promising approach in biology to build better predictive models of diagnosis, prognosis, and therapy at the cellular level of the living creatures. In particular, the recent advances in high-throughput genomic microarray and proteomic technology allow the identification of genes and proteins, or a functionally related cluster of genes and proteins, that may play a major role related to a specific phenotype. With the aid of advanced learning algorithms, analysis of mircroarray data can help to define expression patterns relating to a specific phenotype, and more importantly, to interpret the results to gain insights into the related biological mechanism.
However, in computational biology, investigators are confronted with the high dimensionality problem, i.e. each data sample could be defined by hundreds or thousands of measurements that might be concurrently obtained. For example, it is typically estimated that the human genome consists of up to 25,000 genes. Attempting to extract meaningful expression patterns, and thus to infer related genes and pathways to reveal the underlying biological mechanism from small sets of data in such high dimensional space is incredibly difficult.
This project focuses on the development of discriminative learning algorithms, in particular the support vector machines, for microarray data analysis.
Methods and results
Advanced learning algorithm for support vector machines
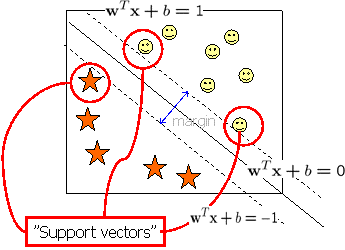
As a class of discriminative approaches, Support Vector Machines (SVMs, see figure 1), which is based on statistical learning theory, have delivered the state-of-the-art performance in diverse real world applications, in particular, computational biology which covers:
- Cancer classification from microarray data
- Gene functional classification
- Protein-protein interaction prediction
- Regulatory module search
- Protein functional classification
- Protein sequence similarity detection
- Splice site recognition
Theoretic research is on the improvement of the SVM algorithms, including
1) Reduction of Support Vectors (SVs) in the expansion of the decision function
Support Vectors (SVs) refer to those training samples whose corresponding Lagrangian multipliers are non-zero. A large number of SVs from training an SVM poses great challenges to prediction abilities of an SVM: 1) it slows down the speed of the SVM to predict the class of unlabelled examples; 2) it increases the likelihood of the SVM to commit prediction errors. The problem is particularly server with microarray data. A two-stage algorithm, which was original developed by the team for the nonlinear dynamic systems, is modified for SV reduction.
2) Development of new multi-class SVMs
Multi-classification tasks are very common in biological world. However, SVMs are originally developed for binary classification and hindered to solve multi-classification directly. Usual approach has been the resolution of the multi-case problem into a series of binary ones. But the universal 1-vs-1 decomposition scheme could lead to a number of binary SVM as the number of binary SVM tends to grow quadratically to that of classes. This places a heavy burden to system resources. Some new methods have been proposed to train multi-class SVMs directly with the aid of regression techniques.
We first propose a new voting approach to the assignment of class label for a test observation after pairwise training of SVM classifiers. The approach investigates the correlations between "scores" - the real valued vector produced for observations by a set of binary SVM classifiers. These score vectors are then combined using a majority voting mechanism to assign the class membership for the test observations. The performance of the algorithm is evaluated on various gene expression profiles, and two typical multi-class SVM algorithms, namely the max-wins voting by Friedman and pairwise coupling by Hastie and Tibshirani, are compared with the proposed method. The experimental results on synthetics data and microarray of real life show the efficacy of the proposed method and that the new multi-class SVM is superior to max-wins and pairwise coupling in terms of the classification of multiple-labeled microarray.
We then develop a new multi-class Least Squares Support Vector Machine (LS-SVM) whose solution is sparse in the weight coefficient of support vectors. The solution of a binary LS-SVM Support Vector Machine (LS-SVM) is constructed by most of training samples, which is referred to as the non-sparseness problem. Multi-class LS-SVMs which are learnt on the basis of binary ones inevitably share the same problem. A direct consequence is the slowdown of the LS-SVM classification on test examples. We addresses this issue by presenting a variant of the binary LS-SVM, in which the spareness of the solution is greatly improved. A new sparse multi-class SVM is developed from the binary case. The training of the LS-SVM method is implemented using an adapted two-stage regression algorithm.
3) Fast learning of least-squares SVM
The optimal separating hyperplane of a typical Least Squares Support Vector Machine (LS-SVM) is constructed using most of the training samples. A consequent disadvantage is the slowdown of the LS-SVM classification process on the test samples. Previous methods address this issue by simplifying the decision rule established after training, which risks a loss in generalization ability and imposes extra computation cost. This paper presents a novel optimal sparse LS-SVM whose decision rule is parameterized by the optimal set of training examples, in addition to having an optimal generalization capability. For a large number of classification problems, the new LS-SVM requires a significantly reduced number of training samples, a property referred to as the sparseness of the solution. The training of the LS-SVM method is implemented using a modified two-stage regression algorithm.
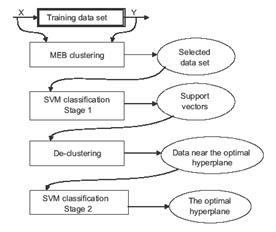
4) Minimum enclosing ball clustering for SVM
It is well known that conventional SVM is not suitable for classi?cation of large data sets due to its computational complexity. To address this problem, a novel approach is proposed for large data sets by using minimum enclosing ball clustering. After the training data are partitioned by the proposed clustering method, the centers of the clusters are used for the ?rst time SVM classi?cation. Then the clusters whose centers are support vectors or those clusters which have different classes are used to perform the second time SVM classi?cation. In this stage most data are removed (see Figure 2).
These above approaches have been used for classification of gene expression profiles for various cancer microarray data sets (Figure 3).
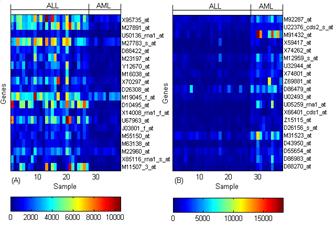
Fig 3. Selected gene expression level (A) Up regulated in ALL (B) Down regulated in ALL
Acknowledgements
This work has been partially supported by the Engineering and Physical Sciences Research Council (EPSRC) for funding this project (GR/S85191/01), the Virtual Engineering Centre, and Queen’s University Belfast International Exchange Scheme.
Publications
- X. Xia, K. Li, G. W. Irwin, “Improved training of an optimal sparse least squares support vector machine”, accepted by the 17th IFAC World Congress, July 6-11, 2008, Seoul, Korea.
- X. Xia, K. Li, “A sparse multi-class least squares support vector machine”, accepted by 2008 IEEE International Symposium on Industrial Electronics, Cambridge, UK, June 30 to July 2, 2008.
- K. Li, X. Li. G. Irwin, G. He (editors), Life system modelling and simulation. Lecture Notes in Bioinformatics, Springer-Verlag GmbH. LNBI 4689, 2007.
- X. Li, K. Li, G. W. Irwin, “A Two-Stage SVM Classifier for Large Data Sets with Application to RNA Sequence Detection”, Neurocomputing, 2007 (under review).
- H. Wang, K. Li, “A New Algorithm Based on Support Vectors and the Penalty Strategy for Identifying Key Genes Related with Cancer”, Transactions of the Institute of Measurement and Control , Vol. 28, No. 3, 263-273, 2006.
- X. Li, K. Li, “A Two-Stage SVM Classifier for Large Data Sets with Application to RNA Sequence Detection Life System Modeling and Simulation”, Lecture Notes in Bioinformatics, Springer-Verlag GmbH, Volume 4689, 2007. 8-20.
- Y-Y Wan, J-X Du, and K. Li, “A Novel Feature Extraction Approach to Face Recognition Based on Partial Least Squares Regression”, Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4113, 2006, 1078-1804.
- S. Pei, D-S Huang, K. Li, and G. W. Irwin, “Gene Selection by Cooperative Competition Clustering”, Computational Intelligence and Bioinformatics, Lecture Notes in Bioinformatics, Springer-Verlag GmbH, LNBI 4115, 464-474, 2006.
- X. Yan, L. Cao, D-S Huang, K. Li, and G. W. Irwin, “A Novel Feature Fusion Approach Based on Blocking and Its Application in Image Recognition”, Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4113, 2006, 1085-1091.
- X. Xia, K. Li, “A New Score Correlation Analysis Based Multi-Class Support Vector Machine For Microarray Datasets”. 2007 International Joint Conference on Neural Networks (IJCNN), Orland, Florida, August 12-17, 2007.
Keynote speech
- G. W. Irwin, K. Li, “Computational Intelligence for Data Modelling with Life Science Applications”, International Conference on Life System Modelling and Simulation, Shanghai, September 14-17, 2007.
