Engineering Genes – A New Genetic Modelling Approach for Modelling of Engineering and Life Systems
Researchers : Dr. Kang Li, Dr Jian-Xun Peng and Dr Patrick Connally
IntroductionThe main theme of this project has been to introduce a new modelling approach through the integration of prior system knowledge in the form of fundamental engineering functions known as ‘engineering genes’ or ‘eng-genes’ in short, into a single-hidden layer neural structure.
Nonlinearity is an inherent property for complex systems in many areas, which arises from the first principle laws and empirical equations that govern the system behaviour. Mathematical modelling based on such priori knowledge usually leads to a set of linear and nonlinear ordinary and partial differential equations, which sometimes can be difficult to solve or requires extensive computing resources or have very limited number of samples (e.g. biomedical data). Obviously this ‘white-box’ method is not applicable for many real-life problems.
Alternatively, data-driven ‘black-box’ methods use much simpler, usually lumped, models to approximate the original systems, allowing the designer to adjust the balance between accuracy and computational complexity by altering the model type and model complexity. For black-box methods, the chosen model, such as multilayer perceptron, radial basis function, polynomial nonlinear autoregressive exogenous model (NARX) and indeed many other approximators, may bear little physical relation to the system and therefore the quality of the resulting model is heavily reliant on the identification data.
A ‘grey-box’ method is utilised in cases where it is desirable to incorporate some of the advantages of both of the white-box and black-box approaches. Depending on how, and how much, the priori engineering knowledge can be used, there exist different grey-box approaches. These though can be categorised into two general classes. The first chooses a conventional black-box model, and ‘priori’ knowledge is used to shape the parameter identification or model structure selection. The alternative is to start with a model originating from the mathematical relations, which describe the behaviour of the system. In the latter approach, physical modelling and system identification form two interacting paths, and most methods would assume that the model structure is known 'a priori', and the major modelling task is then to identify unknown parameters and unmodelled dynamics using black-box models. These two grey-box approaches have limitations when the engineering systems are either too complex to derive a simplified model or that the physical knowledge about the process is incomplete.
Despite many advances in nonlinear system modelling and identification in the literature, the eng-genes method for the first time breaks down a complex nonlinear system into basic (mathematical) elements (fundamental nonlinear functions and operators), namely ‘engineering genes’ from priori engineering knowledge, which are then composed and coded into an appropriate chromosome (model) representation associated with a specific structure (a generalised single-hidden layer neural structure in this project). The chromosome, or a group of chromosomes, then evolves to produce a model which best fits the system with improved performance and transparency.
This team has made substantial progress in the development of the eng-genes concept and associated algorithms and software.
- Initial studies were carried out to investigate the applicability of existing model structure determination and parameter optimisation techniques to eng-genes models. These provided valuable insight into the approximation properties and the training behaviour of these new models, and highlighted areas where current modelling techniques were deficient when applied to this type of model.
- Subsequent work thus concentrated on the development and implementation of novel techniques which allow eng-genes models to be constructed in a more efficient and accurate manner, and simplify the inclusion of available fundamental system knowledge. This includes the analytic discrete and hybrid algorithms for generalised single hidden-layer neural models, and a stand-alone software package using advanced genetic algorithms.
- The eng-genes method and many algorithms have been applied to both simulated and real data sets. I believe that the outcomes of this study represent a significant contribution in the relevant field. Full details of the main achievements are available in the publications arising from this project.
Methods and results
1) Eng-genes modelling concept
The name ‘eng-genes’ derives from the view that basic nonlinear functions act as the fundamental building blocks of system behaviour. These functions can then be seen to be analogous to the genes present in the cells of the body. The model type most closely based upon this concept is the artificial neural network, which attempts to mimic the operation of biological neurons through parallel combinations of simple mathematical structures. The eng-genes concept, therefore, seeks to enhance the transparency and accuracy of neural models by integrating a ‘gene’ of fundamental system knowledge into each artificial neuron in the structure. This work is inspired directly from the original Kolmogorov's superposition theorem which has laid the foundation for the approximation analysis of artificial neural nets. Conventional neural networks derive their approximation capacity from the superposition of simple functions, where the constituent functions are mostly homogenous within the network, and chosen for ease of use and training. Thus, their relevance to the system under study is rarely investigated. Kolmogorov's theorem on the other hand also suggests that the appropriate set of functions is dependent on the system to be modelled. Hence, the natural means of including the system-related nonlinearities fundamental to the eng-genes concept is to use them as activation functions within the hidden layer of the neural model, aiming to improving the model transparency and generalisation performance. Mathematically, an eng-genes neural network used to model a MISO nonlinear system, where the activation function are ‘eng-genes’ or fundamental functions identifiable from first principle laws or empirical engineering equations.
For any neural network topology, the determination of the structure, in terms of the number of inputs and size of the hidden layer, is a necessary stage in the modelling process. However, the inclusion of system-derived nonlinearities as activation functions adds further complexity to the procedure. Firstly, there may in some cases be more potential activation functions available from the system knowledge than are feasible to include in a small, computationally efficient model, or some of the functions may not significantly affect the system's behaviour. In these cases, it is necessary to determine the most dominant and significant functions from the ‘pool’ or the ‘gene library’ collected from systems and processes of similar nature (governed by similar engineering principles and laws). Furthermore, these functions may be parametric, and hence the effectiveness of the neural model will also depend on selecting optimal parameter values. The resulting ‘eng-genes’ modelling procedure is illustrated in figure 1. The concept has been formally introduced in greater detail in publications.
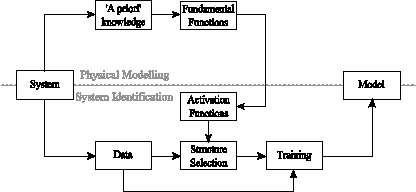
Fig 1. Eng-genes modelling approach
2) Approximation and training analysis of Eng-genes model
This project initially concentrated on the application of existing conventional modelling techniques to eng-genes type networks, in an effort to both investigate the approximation properties of the new networks in comparison with conventional neural nets and to determine the areas in which new techniques would be necessary. One major part of this research effort has been to create the eng-genes networks using evolutionary algorithms like genetic algorithms and genetic programming which can both determines the structure of the network in terms of type and number of hidden-layer neurons and optimise the parameters associated with the activation functions and the network weights. These networks were compared to conventional MLP networks which had been optimised using the same genetic algorithm, and the eng-genes networks were shown to provide better generalisation performance for the application studied.
The earlier work on this aspect also suggested that due to the stochastic sampling and computationally-intensive nature of genetic algorithms, advanced methods and associated software are needed to improve the optimisation speed, otherwise it would not be well suited for practical applications. One proposed means of dealing with this was to ‘split’ the eng-genes modelling process into two steps, whereby the activation functions and their parameters (the ‘structural’ portion) would be determined offline by genetic algorithms. The neural network weights and biases could then be optimised by conventional neural network training techniques, many of which have computationally-efficient online variants.
The question thus arising regards the effectiveness of conventional neural network training algorithms when applied to networks utilising non-conventional activation functions. This issue was first approached by means of a case study, in which heterogeneous neural networks which had been previously structurally optimised via the use of genetic algorithms were trained from random starting points using the well-known Levenberg-Marquardt algorithm. While this work showed that eng-genes networks are capable of comparable or superior performance to conventional MLP's, a significant issue was raised. Specifically, it was found that in some cases, the eng-genes networks were more susceptible to unstable performance under parallel operation than similar MLP networks. To further investigate this phenomenon, this team examined the effect of nonconventional activation functions on the performance of standard (in this case gradient-based) neural network training algorithms. The chosen approach was to model simple target systems with very small neural networks, such that the correct choice of activation functions and network parameters would produce an exact match between system and model. The simplicity of the problem allowed for large numbers of networks to be trained for each system-model pair, resulting in meaningful statistical analysis of the difference between conventional and eng-genes-type neural networks. In addition, the small dimensionality of the problem allowed for visualisation of the solution space, giving an intuitive insight into the issues involved. Examination of both the statistics and the plotted surfaces resulted in the stability difficulties being addressed with a novel scheme combining prediction-error-based training with simulation-error-based training4.
3) Advanced algorithms and software for eng-genes model construction and training
Several new algorithms were derived and a standalone software package was developed.
- Discrete and mixed discrete-continuous eng-genes modelling algorithms
Through the course of the research, it became clear that advanced analytic methods are desirable for practical implementation of ‘eng-genes’ modelling due to their computational efficiency. However, the particular demands of eng-genes modelling, incorporating activation function selection, network structure determination and optimisation of both function and network parameters, proved beyond the capabilities of existing algorithm or framework. Clearly, the development of such an algorithm became a priority. The biggest challenge was that the eng-genes model is a heterogeneous neural network and the activation functions extracted directly from engineering priori knowledge can be difficult to train using conventional methods. Therefore, it was found to be beneficial to view the eng-genes concept as a ‘superset’ capable of comprising several other types of nonlinear model, at least from a mathematical perspective. For instance, RBF neural networks could be viewed as a special case of the eng-genes model in that only one type of hidden node is utilised, but possessing parameters inherent to both the nodes and to the network itself. Similarly, the creation of nonlinear autoregressive models with exogenous inputs could be viewed as a process analogous to the selection of nodes and determination of output weights in an eng-genes network, with the simplifying factor of pre-determined inherent parameters. Hence, rather than being approached as one very complex optimisation procedure, the desired algorithm could be built up by deriving suitable new techniques for each aspect of the process, with the added benefit that each would be novel and useful for a variety of applications and model types in its own right. The final eng-genes implementation could then be achieved by tightly integrating them together into a single efficient scheme.
So, more formally, the task at hand became both the selection of the activation function for each neuron, and the optimisation of the neuron's entire parameter set. In our research, the first step in this process was taken, when a novel fast algorithm for the selection of terms (hidden nodes with pre-determined parameters) and identification of linear parameters (output weights) in nonlinear models was introduced. When used in the creation of NARX models, this algorithm represents a significant improvement over the conventional Orthogonal Least Squares (OLS) algorithm in terms of both computational efficiency and numerical stability. As with all forward stepwise approaches of this type, the fact that the term selection is not exhaustive is the key to its efficiency. However, its result is not optimal. In order to address this issue, the forward term selection was supplemented by a backwards refinement scheme. Once all initial model terms have been selected, each is analysed in terms of its significance to the final model. Insignificant terms are replaced, resulting in a model with improved performance and model compactness. The term selection and subsequent refinement are both performed within a well-defined regression scheme, thus facilitating their integration with further techniques into an overall structure and parameter optimisation scheme for nonlinear models in general and eng-genes networks in particular.
While the issue of selecting the activation functions (or model terms) from a candidate pool was thus resolved, there remained the problem of determining their associated parameter sets. This was first addressed using a continuous forward algorithm for both the construction and optimisation of a general class of nonlinear model was introduced, and, in this case, applied to RBF neural models. The network grows by adding one node each time, and at each stage of construction, the new node is created ‘from scratch’ and its parameters are optimised via conjugate gradient method, with the linear output weight being determined by substituting the least-squares solution into the cost function. It was then noticed that the network performance could be further improved by introducing a hybrid forward algorithm, where the initial nodes are selected from a small pool of candidates and the node parameters are then optimised using second order Newton method, leading to a more comprehensive network construction algorithm. The efficiency of the schemes was confirmed by computational complexity analysis, and simulation results show it to typically outperform alternative techniques both in terms of computation time and model accuracy. Moreover, again to improve the compactness of the model obtained from the forward network construction, a two-stage mixed discrete-continuous method was proposed to allow the refinement of the network constructed in the forward phase9, and a new Jaccobian matrix has been introduced for more accurate training of generalised single hidden layer neural nets (including eng-genes) with significantly improved perofmrance10.
These core algorithms have then been extended and applied to various issues for the eng-genes neural modelling, and more broadly, the construction of generalised single-hidden layer networks, including the input selection, the creation of eng-genes networks, integrated framework for network construction , and real-time network construction, etc. The application studies showed that the eng-genes networks considerably outperform conventional MLP networks when network sizes were kept small. Here it must be noted that in order to maintain the transparency and interpretability of eng-genes networks, smaller network sizes are preferred in any case.
4) Advanced genetic algorithm, eng-genes software and applications
In parallel to the development of the analytic framework for eng-genes neural modelling, this team has also devoted effort to create the eng-genes networks using genetic algorithms, which can both determines the structure of the network in terms of type and number of hidden-layer neurons and optimise the parameters associated with the activation functions and the network weights. Firstly, adaptive bounding techniques were introduced into conventional genetic algorithm to enhance the searching speed and capability. Then a significant amount of effort was devoted to the development of user-friendly software to implement the eng-genes modelling procedure. From a practical standpoint, this software can be used for the creation and optimisation of various neural networks including multilayer perceptron, radial basis function and naturally the eng-genes networks via genetic algorithms. In this software, each network in the population is encoded into a mixed-type chromosome. The first half of the chromosome contains integer values representing the network structure in terms of the type and number of hidden nodes. The second half contains floating-point values, representing network weights and activation function parameters. The software provides flexibility in the effective use of available data, in that the user may select any data segment for modelling via a sliding window. Several options exist for visualisation of the optimisation process, allowing the user to
- access project and parameter information
- plot training and validation data
- view populations and their properties along the evolution process
- view a selected chromosome in its decoded form and
- view the network estimation performance of any member of the population over a given dataset
The software also provides functionality to transfer optimised networks to the Matlab environment. In addition, both the discrete and continuous forward selection algorithms have been implemented within the Matlab environment, allowing for a deterministic alternative to the genetic algorithm software for eng-genes network creation and optimisation. A sample screenshot of the software's user interface is shown in figure 2.
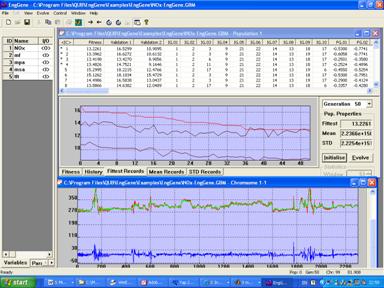
Fig 2. Sample screenshot of the software for eng-genes modelling
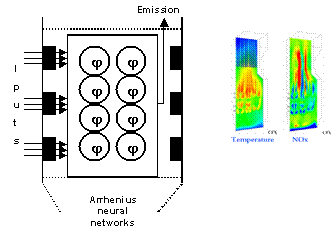
The publications produced in the course of the project demonstrate several potential application areas. Additionally, one stated aim of the investigation work into the eng-genes concept was the establishment of a ‘library’ of potential activation functions. The publications describe both numerous examples of such stock functions, as well as the process by which further such functions may be derived from the available system knowledge. The eng-genes concept and many derived algorithms have been applied to both simulated data and real plants, such as estimating the NOx emission levels from several thermal power plants in UK and Italy (figure 3) and estimation of emissions in urban air in Belfast, modelling of a pH neutralisation process from real data, etc. The methods and algorithms have also been applied to systems biology in modelling the signalling pathway, bioinformatics in cancer gene detection and classification, nonlinear system control using eng-genes network, nonlinear system modelling using multiple neural nets, network based identification and control, and rule selection for fuzzy modelling, etc.
Acknowledgements
This work has been supported by the Engineering and Physical Sciences Research Council (EPSRC) for funding this project (GR/S85191/01), and European Social Fund.
Keynote speech
- G. W. Irwin, K. Li, “Computational Intelligence for Data Modelling with Life Science Applications”, International Conference on Life System Modelling and Simulation, Shanghai, September 14-17, 2007.
- K. Li, “General Introduction to Nonlinear System Modeling & Identification”, 18th International Conference and Fair for Measurement Instrumentation and Automation, Everbright Exhibition Centre, Shanghai, 19 September, 2007.
Invited lectures
- The University of Sheffield , “Construction and training of generalised single hidden-layer neural networks”, 31 Oct, 2007, Sheffield, UK.
- University of Iowa . “Advanced generic algorithm for nonlinear system modelling and optimisation”, 3 July, 2007, Iowa City, USA.
- National University of Singapore , “A new subset selection algorithm for identification of nonlinear dynamic systems”, 12 July, 2006, Singapore.
- Nanyang Technological University , Singapore, “A new subset selection algorithm for identification of nonlinear dynamic systems”, July 4, 2006, Singapore.
- Polytechnic University of Bari , “Intelligent System Modelling and Control with application to some environmental issues”, March 27-31, 2006, Taranto, Italy.
- Shanghai University , “A new subset selection algorithm for identification of nonlinear dynamic systems”, 3 August, 2006, Shanghai, China.
- Shanghai Jiaotong University , “Eng-genes: a genetic modelling approach for nonlinear dynamic systems”, April 04, 2005, Shanghai, China.
- Institute of Intelligent Machines, Chinese Academic of Sciences, “Eng-genes: a genetic modelling approach for nonlinear dynamic systems”, April 08, 2005, Hefei, China.
- Shangdong University , “Eng-genes: a genetic modelling approach for nonlinear dynamic systems”, April 12, 2005, Shandong, China.
- University of Glamorgan , “A grey-box approach for nonlinear dynamic system modelling and identification”, Nov. 19, 2004, UK.
- Shanghai Jiaotong University , ‘Nonlinear dynamic system modelling and identification using grey-box methods’, June 21, 2004, Shanghai, China.
- Shanghai University , ‘‘Nonlinear dynamic system modelling and identification using grey-box methods’’, June 24, 2004.
Journal papers
- J. Peng, K. Li, G. W. Irwin. “A new Jacobian matrix for optimal learning of single-layer neural nets”. IEEE Transactions on Neural Networks Vol. 19, No.1, 119-129, 2008.
- J. Cervantes, X. Li, W. Yu, K. Li. “Support vector machine classification for large data sets via minimum enclosing ball clustering”. Volume 71, Issues 4-6, Pages 611-619 , 2008.
- J. Peng, K., S. Thompson, P. A. Wieringa. “Distribution-based adaptive bounding genetic algorithm for continuous optimisation problems?”. Applied Mathematics and Computation., Vol 185: 1063–1077, 2007.
- K. Li, J. Peng, S. Thompson, “Genetic neural modeling of pollutant emissions from thermal power plants”, Dynamics of Continuous, Discrete and Impulsive Systems Series B: Applications & Algorithms, Vol. 14 (S1), pp 48-56, 2007.
- P. Connally, K. Li, G. W. Irwin. “Prediction- and simulation-error based perceptron training: solution space analysis and a novel combined training scheme”. Neurocomputing Vol 70, 819-827, 2007.
- J. Peng, K. Li, G. W. Irwin. “A novel continuous forward algorithm for RBF neural modelling”, IEEE Transactions on Automatic Control, Vol 52, No.1, pp. 117-122, 2007.
- K. Li, J. Peng. “Neural Input Selection – A fast model based approach”. Neurocomputing , Vol 70, pp 762-769, 2007.
- P. Connally, K. Li, G. W. Irwin. “Integrated structure selection and parameter optimisation for eng-genes neural models”, Neurocomputing, 2007 (available online).
- X. Hong, R.J. Mitchell, S. Chen, C. J. Harris, K. Li, G. W. Irwin. “A survey on nonlinear system identification algorithms”. International Journal of Systems Science (submitted), 2007.
- P. Gormley, K Li, G. W. Irwin, “Modelling the MAPK Signalling Pathway using a 2-Stage Identification Algorithm”, Systems and Synthetic Biology (in print), 2007.
- K. Li, J. Peng, E-W Bai. “Two-stage mixed discrete-continuous identification of Radial Basis Function (RBF) neural models for nonlinear systems”. IEEE Transactions on Circuits & Systems, (submitted).
- K. Li, J. Peng, “System oriented neural networks – problem formulation, methodology, and application”, International Journal of Pattern Recognition and Artificial Intelligence , Vol. 20, No. 2, 143-158, 2006 .
- K. Li, J. Peng, E-W Bai. “A two-stage algorithm for identification of nonlinear dynamic systems”. Automatica, Vol. 42, No 7, pp. 1189-1197, 2006.
- J. Peng, K. Li, D.S. Huang. “A hybrid forward algorithm for RBF neural network construction”. IEEE Transactions on Neural Networks, Vol 17, No. 6, pp 1439-1451, 2006.
- K. Li, J. Peng, G. Irwin, “A fast nonlinear model identification method”, IEEE Transactions on Automatic Control, Vol. 50, No. 8, 1211-1216, 2005.
Conference papers
- K. Li, “Eng-genes: a new genetic modelling approach for nonlinear dynamic systems”, IFAC World Congress on Automatic Control, July 3-8, 2005.
- J. Peng and K. Li, “A novel GA-based neural modelling platform for nonlinear dynamic systems”, IFAC World Congress on Automatic Control, Prague, July 3-8, 2005.
- K. Li, J. Peng, G. W. Irwin, L. Piroddi, W. Spinelli. “Estimation of NOx emissions in thermal power plants using eng-genes neural networks”. IFAC World Congress on Automatic Control 2005, Prague, July 3-8, 2005.
- P. Connally, K. Li, G. Irwin, “Two applications of eng-genes based nonlinear identification”, IFAC World Congress on Automatic Control 2005, Prague, July 3-8, 2005.
- K. Li, J. Peng, M. Fei, X. Li, and W. Yu. “Integrated analytic framework for neural network construction”. Advances in Neural Networks - ISNN 2007, Lecture Notes in Computer Science, Vol. 4492, June 3-7, 2007, Nanjing, China.
- K. Li, Jian-Xun Peng, Minrui Fei. "Real-time construction of neural networks". Artificial Neural Networks – ICANN 2006. Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4131, 2006, 140-149.
- K. Li, B. Pizzileo, A. Ogle, and C. Scott, “Staged neural modeling with application to prediction of NOx pollutant concentrations in urban air”, Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4113, 2006, 1282-1293.
- X. Xia, K. Li, “A new score correlation analysis based multi-class support vector machine for microarray datasets”. 2007 International Joint Conference on Neural Networks (IJCNN), Orland, Florida, August 12-17, 2007.
- P. Connally, K. Li, G. W. Irwin, Shuzhi Sam Ge. “Nonlinear adaptive control using Eng-genes neural networks”, International Conference Control 2006, Glasgow, Scotland, August 30 to September 1, 2006.
- B. Pizzileo, K. Li, “A new fast algorithm for fuzzy rule selection”, IEEE International Conference on Fuzzy Systems, Imperial College, London, UK, 23-26 July, 2007.
- B. Pizzileo, K. Li, and G. W. Irwin. “A fast fuzzy neural modelling method for nonlinear dynamic systems”. Advances in Neural Networks - ISNN 2007, Lecture Notes in Computer Science, Volume 4491, Springer, 2007, 496-504.
Conference proceedings
- K. Li, M. Fei, G. Irwin, S. Ma (editors), Bio-inspired computational intelligence and applications. Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4688, 2007. K. Li, X. Li. G. Irwin, G. He (editors), Life system modelling and simulation. Lecture Notes in Bioinformatics, Springer-Verlag GmbH. LNBI 4689, 2007.
- D. S. Huang, K. Li, G. W. Irwin (editors). Advances in Intelligent Computing, Lecture Notes in Computer Science, Springer-Verlag GmbH. LNCS 4113, 2006; Computational Intelligence, Lecture Notes in Artificial Intelligence, Springer-Verlag GmbH, LNAI 4114., 2006; Computational Intelligence and Bioinformatics, Lecture Notes in Bioinformatics, Springer-Verlag GmbH, LNBI 4115, 2006; Intelligent Control and Automation, Lecture Notes in Control and Information Sciences, LNCIS 344, Springer-Verlag GmbH, 2006; Intelligent Computing in Signal Processing and Pattern Recognition, Lecture Notes in Control and Information Sciences, LNCIS 345, Springer-Verlag GmbH, 2006.
