Introduction

A mesh is a set of elements of simple shape whose assembly represents a calculation domain for a numerical solution of a set of PDEs. The use of block-structured meshes generally give favourable performance of numerical solvers. However, the absence of robust effective methods for automatically generating multi-block decompositions of geometries means that the task must be done interactively by the analyst, which for complex geometries can be time consuming and tedious.

Research Objectives

The objective of this research is to develop methods for generating multi-block decompositions of 2-D and 3-D geometries. The methods should be:

  1.   Theoretically sound,

  2.   Implementable in an automated algorithm,

  3.   Capable of producing simple decompositions on which high quality meshes can be generated, and

  4.   Controllable, i.e. allow for addition optional inputs to adjust the solution.

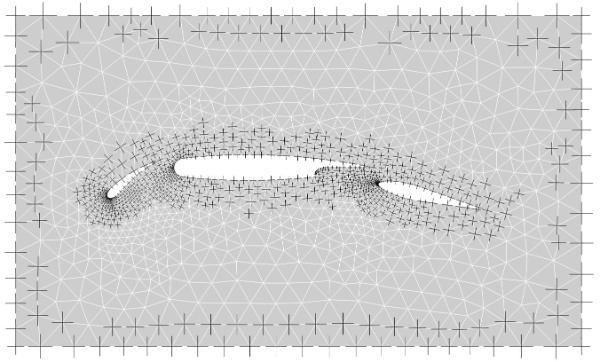
Decomposition Method

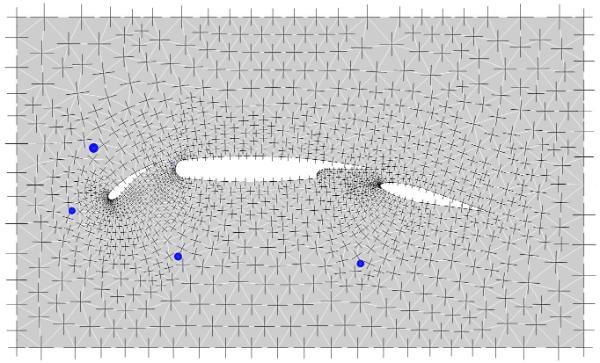
Step 2. Mesh singularities are identified in tri elements by a simple check.

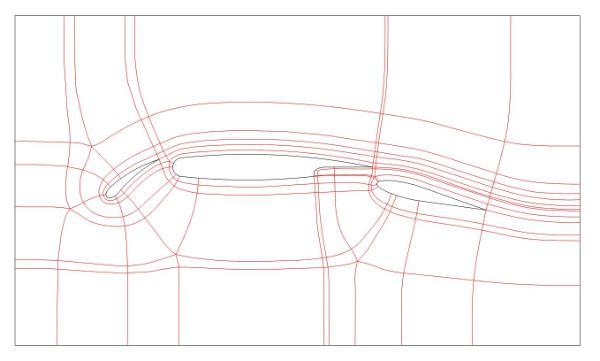
Step 3. Critical cross-field streamlines are traced from singularities and geometry corners thus partitioning the geometry into rectangular blocks.

Step 4. The final block-structured quad mesh is generated on the multi-block decomposition by solving a integer programming problem for the division numbers and utilising simple mapped meshing algorithms.

The method is effective on planar and curved surfaces of arbitrary genus.

Conclusions

A novel method has been developed for automatically generating multi-block decompositions of surfaces for boundary conforming block-structured meshes. Mesh singularities occur naturally as a result of incompatible alignment constraints or significant Gaussian curvature in isolated positions near the medial axis. Recent progress has been the incorporation of target input mesh sizes and directions in the algorithm. There is an obvious extension of the methods to 3-D geometries for automatic hex mesh generation.